Overview

In the previous lessons, we focused on hacking two-dimensional (2D) games. While many of the techniques we have covered can be applied to any game, there are unique techniques that only apply to three-dimensional (3D) games. To make hacks like wallhacks or aimbots for 3D games, we need to understand how 3D games actually work.

Coordinates

When we say a game is 2D, we are referring to the fact that all objects in the game can be located by a coordinate pair. These coordinate pairs contain two values: X (horizontal position) and Y (vertical position). Coordinate pairs are usually referenced with parentheses around them, like (X, Y).

Using the screenshot from Wesnoth as an example below, let’s imagine we had a point (0, 0) in the bottom-left of the screen and a point (10, 10) in the top-right. The highlighted unit could be represented by the coordinate (7, 5) and the un-highlighted unit could be represented by the coordinate (3, 1).

The game uses these coordinates for many critical operations. For example, when a player attempts to move, the game will verify that the player’s new coordinates will not be in water or impassable terrain. All 2D games use coordinates in this manner, whether the game has a top-down or side view.

3D Space

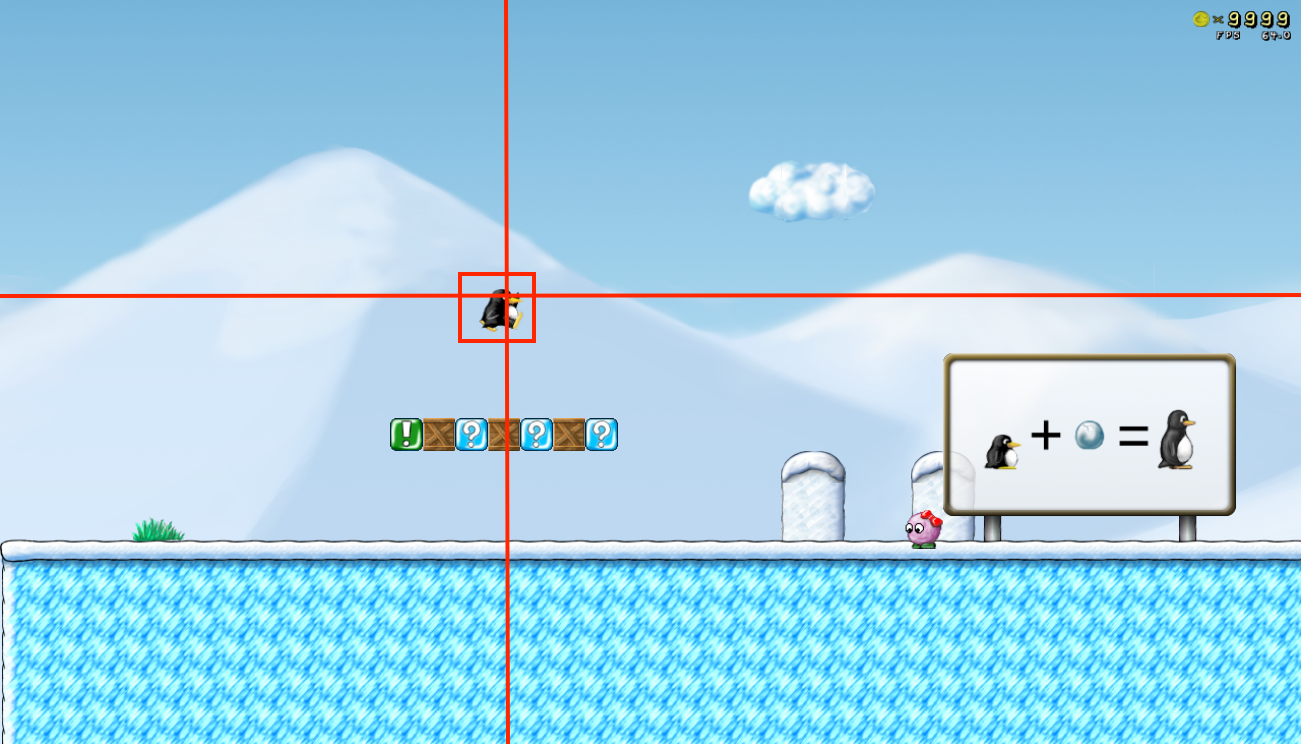
When playing Wesnoth, one thing you may notice is that two units can never share the same coordinates. This is because the game would not be able to properly display each unit to the player without having special logic to handle switching between the two images. However, in 3D games, two units can share the same horizontal and vertical coordinates.

As you can see, the other player and our current player are both in the middle of the screen and have the same (X, Y) values. However, in 3D games, coordinates are represented with three values: X, Y, and also Z (depth). In the example above, both players could be at (5, 5) in 2D space, but their 3D coordinates could be (0, 0, 0) and (0, 0, 5).

Cartesian Coordinates

One of the easiest ways to understand the relationships between coordinates is through the use of Cartesian coordinate systems. For example, we could graph our first Wesnoth example like so:

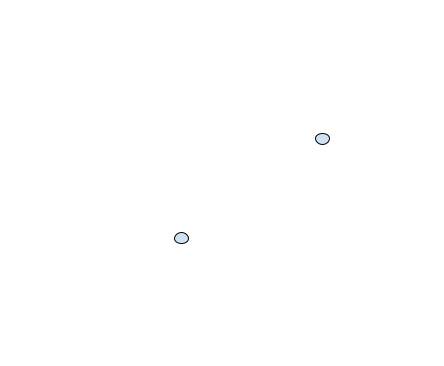
The strength of visualizing the coordinates like this is that we can then use normal geometric operations. Let’s say we wanted to get the distance between these two units. By creating a right triangle from the two units, we can use the Pythagorean theorem to calculate that triangle’s hypotenuse. Due to the way we created this triangle, this hypotenuse would represent the distance between these two units:

3D coordinates can also be graphed with the addition of another axis. Our 3D game example above might be graphed like:

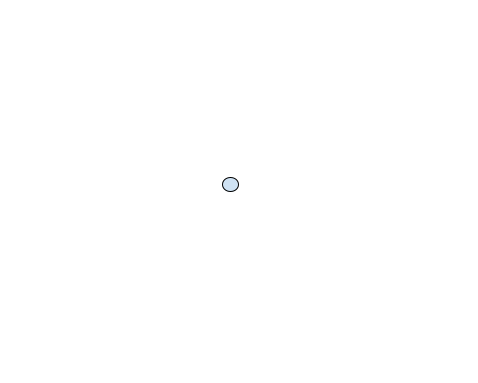
Notice how, despite each player having identical X and Y coordinates, they exist in different places on the graph.

Viewports

Monitors display a 2D image on a flat screen. Therefore, it is impossible for monitors to render a 3D scene directly. Instead, the 3D world must be converted into a 2D scene, like taking a picture. Games will often have functions for this, typically called some variation of WorldToScreen. Sometimes, when programming hacks such as displaying text above a player’s head, you will need to write this code yourself. In the ESP lesson, we will discuss how to write this code for any game.

A key aspect of 3D-to-2D conversion is that games will choose a viewport, or a view into the game’s world. This will often be the current player’s view, but in games that support free cameras, this could be any position. For this viewport, the game will then calculate the depth for all objects in the scene. It will also draw objects that are farther away “behind” objects that are closer. For example, in the following viewport, the game first draws the building in the background. It then determines that the trees are in “front” of the building in the current viewport and draws them on top of the building. In this way, the game achieves the illusion of depth.

3D Movement

Operations in 3D space are expensive to compute. Because of this, games will often take several shortcuts to optimize their performance. One these shortcuts is always placing the player at the origin, or point (0, 0, 0). This way, all distances and angles for objects can be calculated by just retrieving that object’s coordinates instead of having to subtract the object’s position from the player’s position. However, if the player is stuck at (0, 0, 0), they will be unable to move. To achieve the illusion of movement, some games will instead rotate the entire world around the player. For example, if you press the key to move forward, the game will respond by moving the whole world toward you instead of moving your player forward. Not all games work like this, but several well-known ones use this model.